I’ve done a hyperparameter search and found that shallower models are drastically easier to optimize. The thing with orderless NADE is that the random masking of the input adds a lot of noise to the optimization process, and as a result it is practically impossible to overfit anything.
I’m also exploring the use of discrete Earth Mover’s Distance as the loss instead of the hopelessly categorical cross-entropy. Optimization is much smoother with EMD, and I can imagine the gradient points toward more reasonable regions of hyperparameter space. I’m running a new hyperparameter search with three different losses – cross entropy and two variants of EMD with L1 and L2 distance – in order to qualitatively compare the models they produce.
I’ve messed with residual and dilated convolutions but no particular luck. Dilated convolutions seem like a good fit though in order to bridge the 32x32 gap with fewer layers. The whole thing runs about 3x as fast with dilated convolutions, all else equal.
Below are some samples from a shallow EMD L1 model. First, Gibbs samples:
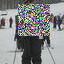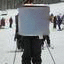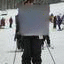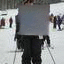











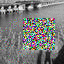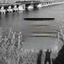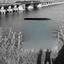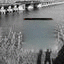







I was also interested to see how ancestral samples look. For ancestral sampling, one has to choose an ordering according to which to sample. I tried three cases: orderless (random) ordering, greedy ordering (sample the variable with the lowest entropy first), antigreedy ordering (sample the variable with the highest entropy first).
Antigreedy ordering seems like a strange thing to do, but in our music work we found that this ordering got dramatically better log likelihood scores when evaluating validation data points. I had a hunch this is an artifact of teacher-forcing, where after making its prediction the model would get to see the ground truth for that variable; of course you want to get the ground truth of the things you’re most uncertain about. However I was never sure whether it would also help during generation.
Orderless:




















Greedy:



















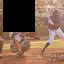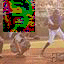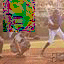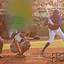
Antigreedy:




















Interestingly, the greedy ordering does not work outward-in as much as I expected it to. Also antigreedy seems to be the only strategy here that succeeds at generating some structure. I believe the overall failure to do this is due to the model learning only very local relationships. At training time, I draw fully random masks and so there are always some nearby unmasked pixels for the model to depend on. I will experiment with training with large contiguous masks instead.