As promised in the last post, I’ve been working on more contiguous forms of masking to de-emphasize trivial local correlations when training the model. I’ve tried masking a randomly positioned 32x32 rectangle, just like I do at generation time, but the results are terrible and I feel like it’s too much. Here are some samples from a model trained on squared EMD with 32x32 rectangular masks:
| Strategy | Samples |
|---|---|
| Greedy |





|
| Antigreedy |





|
| Orderless |





|
| Gibbs |




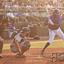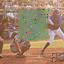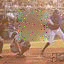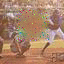
|
There’s another approach I’d like to explore, in which I stick with the idea of using independent Bernoullis to decide what to mask out, but instead of taking them as-is I mask out a whole neighborhood around each masked-out variable:
I mask out the neighborhood by taking a conjunction of translations of the Bernoulli mask. This increases the number of variables masked out, so in order for $p$ to have the same meaning I must use a transformed value $q$ such that
\[p = q^a\]where $a$ is the area of the neighborhood (including the center).
There’s another technicality to take care of. The masks for plain orderless NADE are chosen so that the size of the mask is uniformly distributed. This is done to ensure that conditional distributions with very many or very few variables in the condition (these would be rare under a binomial distribution) are sampled just as frequently as the more common ones.
An obvious way to enforce uniform mask size with plain Bernoullis is to sample a mask size $k$ and then use np.random.choice to decide which $k$ variables to mask out (or, as I’ve been doing in Tensorflow, create a mask with $k$ ones in the front and then shuffle it).
It’s not obvious how to do this in the presence of potentially overlapping neighborhoods. However, a miracle has our backs.
As already stated, given Bernoulli masking probability $p$, the mask size $k$ follows a binomial distribution:
\[\Pr(k | p) = \binom{n}{k} p^k (1 - p)^{n - k}\]If only we could find some prior distribution over $p$ to make the expectation uniform, i.e. we want that
\[\int_0^1 \Pr(k | p) \Pr(p) dp = \frac{1}{n + 1}\]where $n + 1$ is the number of possible values $k$ can take on. The miracle occurs when we let $Pr(p)$ be the uniform distribution on the unit interval. Then
\[\begin{align} \int_0^1 \Pr(k | p) \Pr(p) dp &= \int_0^1 \binom{n}{k} p^k (1 - p)^{n - k} dp \\ &= \binom{n}{k} \int_0^1 p^k (1 - p)^{n - k} dp \\ &= \binom{n}{k} B(k + 1, n - k + 1) \\ &= \binom{n}{k} \frac{\Gamma(k + 1) \Gamma(n - k + 1)}{\Gamma(n + 2)} \\ &= \frac{n!}{k!(n - k)!} \frac{k! (n - k)!}{(n + 1)!} \\ &= \frac{1}{n + 1}. \end{align}\]where $B$ is the Beta function.
Putting everything together, I sample a probability $p \sim U(0, 1)$, compute $q \gets p^{1 / a}$, sample a mask according to independent Bernoullis with probability $q$, and conjoin $a$ local translations of the mask to obtain a contiguish mask.
Results to follow.